Astronomija, nauka koja obuhvata proučavanje svih objekata i pojava van Zemlje. (Encyclopaedia Britannica)
Novogodišnji praznici su prošli, vreme je da se radi. Podugački tekst koji sledi predstavlja lagani presek posla koji tiho napreduje već neko vreme. Šta će od svega biti, videćemo. Meni je zabavno, što i vama u svakom slučaju želim.
Rotacija Zemlje oko Sunca. Kažemo da Zemlja kruži oko Sunca. Ovakva kratka izjava znači sledeće: Sunce, jedna od zvezda galaksije Mlečni put, i Zemlja, jedna od planeta lokalnog planetarnog sistema koji nazivamo Sunčev sistem, kreću se (u odnosu na udaljene, fiksne zvezde) oko zajedničkog centra gravitacije. U slučaju Sunca i Zemlje, zajednički centar gravitacije se praktično nalazi u centru Sunca, tako da se u ovom smislu Sunce praktično ne kreće. Zemlja se (gledano sa Sunca) kreće po putanji koja je, istorijski govoreći, prvobitno opisana empirijskim zakonima koje je ustanovio Johan Kepler (koristeći podatke koje je, osmatrajući nebeska tela, sakupio Tiho Brahe). Keplerovi zakoni postuliraju da se Zemlja (gledano sa Sunca) kreće po elipsi u čijoj se jednoj od žiža nalazi Sunce, te da linija koja spaja centar Sunca i centar Zemlje u jednakim vremenskim intervalima prebriše jednake površine – što zapravo znači da se Zemlja (gledano sa Sunca) kreće brže što je njen položaj bliži Suncu, i obratno. Keplerovi zakoni su u saglasju sa Njutnovim zakonom gravitacije, odličnim teorijskim objašnjenjem kretanja (gledano sa Sunca) svih planeta izuzev Merkura.
Nota bene: Čitalac će možda smatrati moje insistiranje na gledanju sa Sunca dosadnim. No, da budemo načisto: jedan od suštinskih razloga za traljavo znanje fizike koje naše škole pružaju jeste olako prelaženje preko relativnosti svih kretanja u prirodi. Zapamtimo da bezuslovno uvek kada o nekom kretanju razmišljamo moramo pre svega da se odlučimo u odnosu na šta to kretanje posmatramo.
Putanja kojom se Zemlja kreće oko Sunca naziva se ekliptika, i obično se crta baš onako kako mali Mikica zamišlja elipse: izdužena zatvorena kriva linija čija je jedna dimenzija znatno veća od druge. Tačka u kojoj je Zemlja najbliža Suncu naziva se perihel, i u našoj epohi Zemlja je doseže otprilike 4. januara. Tačka u kojoj je Zemlja najdalje od Sunca naziva se afel, i u našoj epohi Zemlja je doseže otprilike 4. jula. No, stvarnost je unekoliko drugačija. Sledeća slika prikazuje Zemljinu orbitu oko Sunca i samo Sunce u razmeri 1:1.
Vidimo, Zemljina orbita oko Sunca je zapravo skoro odličan krug. Na gornjoj slici je pravi krug i ucrtan, što se vidi po blago debljoj levoj strani zatvorene linije. Nije cilj ovog teksta da natrpava podatke. Zato ćemo ovde samo reći da je poluprečnik Zemljine orbite otprilike stotinu puta već od prečnika Sunca, te da je Zemlja u svojoj najudaljenijoj tački od Sunca udaljena 3% više nego u najbližoj. To su fine razlike koje oučavamo i koje ipak značajno utiču na klimu na Zemlji.
Nota bene: (Geo)političke i ostale religijske organizacije nas izdašno bombarduju homocentričnim posmatranjem društvenih i prirodnih pojava. Potrošimo malo vremena, pogledajmo ponovo gornju sliku. Mi smo zanemarljiva mrlja na oko-sićušne-tačke-motajućoj zanemarljivoj mrlji, sposobna da sve to i shvati. Ovo nije razlog ni za očaj ni za slavlje. Mi smo to što jesmo, i krajnje je vreme da odrastemo i počnemo da živimo saglasno onome što jesmo.
Godišnja doba. Naša matična planeta Zemlja, tokom svog kretanja oko obližnje zvezde koju zovemo Sunce, menja položaj na takav način da različiti delovi njene površine bivaju više ili manje osunčani (na udaru Sunčeve energije) što obično prikazujemo sledećom slikom:
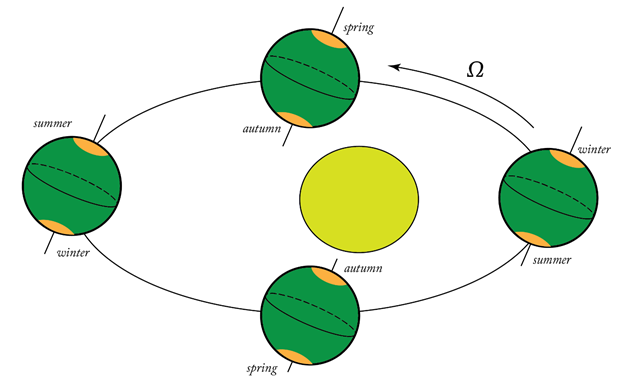
Na slici vidimo četiri karakteristična položaja koja Zemlja zauzima tokom godišnje rotacije oko Sunca. Levi i desni položaj je solsticij, dok gornji i donji položaj nazivamo ravnodnevnica. Iz istorijskih razloga (dominantnih priloga tzv. zapadne civilizacije nauci), redom se sa desna nalevo ovi položaji zovu zimski solsticij (22. decembar), prolećna ravnodnevnica (21. mart), letnji solsticij (22. jun) i jesenja ravnodnevnica (23. septembar). Odgovarajuća godišnja doba počinju upravo tokom naznačenih dana.
Nota bene: datumi su ovde dati orijentaciono i važe samo za našu epohu, jer tanani uticaji koje je teško grupisati i numerički izraziti menjaju ove datume od godine do godine, ali ne dalje od par dana.
Slika prikazuje i osnovni razlog za prepoznavanje godišnjih doba: promena u osunčanosti Zemlje. U okolini zimskog solsticija vidimo da je severna polulopta Zemlje izložena Sunčevim zracima tako da oni stižu pod oštrim uglom – odnosno, drugačije rečeno, Sunce se pojavljuje niže na nebu. Takođe, na delu je efekat koji opisuje drugi Keplerov zakon: pošto je Zemlja u zimskom solsticiju bliža Suncu, ona se brže kreće, što se projektuje u brže Sunčevo kretanje po nebu – stoga obdanica traje kraće.
Rotacija Zemlje oko sopstvene ose. Zemlja, osim rotacije oko Sunca, izvodi i rotaciju oko sopstvene ose rotacije. Pošto ravan Zemljinog ekvatora zaklapa sa ekliptičkom ravni ugao od 23,4°, a osa sopstvene rotacije Zemlje je normalna na ravan Zemljinog ekvatora, obično kažemo da je Zemljina osa sopstvene rotacije nagnuta pod uglom od 23,4°. Ta osa, prirodno, prolazi kroz Zemljine polove i u našoj epohi je usmerena ka zvezdi Severnjači.
Nota bene: ova činjenica je veoma bitna. Uspeh zapadne civilizacije se u dobroj meri zasniva na moreplovstvu, koje je imalo uspeha upravo zato što je zvezda Severnjača najbolji nebeski marker koji je moguće imati – dovoljno je i sjajna i usamljena na severnom nebu.
Za praktične potrebe godišnjih proračuna, možemo reći da osa sopstvene rotacije ostaje sama sebi paralelna tokom godine. No, na duže, milenijumske staze ova izjava nije tačna.
Precesija. Pravac Zemljine ose sopstvene rotacije nije stabilan, već se menja tokom vremena. Kažemo da Zemljina osa sopstvene rotacije izvodi precesiju, odnosno rotira u odnosu na udaljene (praktično stalne) zvezde. Precesiono kretanje je posledica zakona o održanju momenta impulsa, koji se može odlično simulirati pomoću čigre (a klizači na ledu ga izdašno koriste za pravljenje raznoraznih kerefeka).
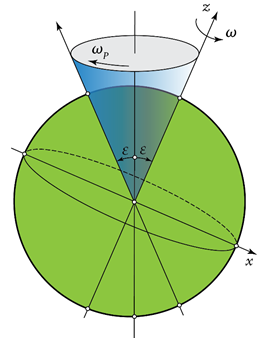
Precesija je prilično spor proces za ljudske standarde: ceo precesioni krug osa sopstvene rotacije Zemlje obavi za nekih 26 hiljada godina. Ovo znači da je u našim krajevima pre 13 hiljada godina leto počinjalo onog dana kada nama počinje zima, da je pre 6500 godina leto počinjalo kada nama počinje proleće (ove dve izjave treba shvatiti uslovno: klima je tada bila značajno drugačija nego sada, i teško je olako praviti paralele), kao i da se Zemljina osa sopstvene rotacije pomerila za nekih 30° od vremena Aristotela do danas. Otuda, kompletna priča koju ovde pričamo važi za našu epohu, vreme od (u odnosu na danas) nekih prethodnih i budućih hiljadu godina.
Nota bene: Spomenimo ovde još samo da su precesija i slični spori procesi, koji ne utiču na naš svakodnevni život, razlozi za postavljanje Milankovićeve teorije klimatskih promena. Posledični Milankovićev godišnji kalendar je klasičan primer pucanja topom u vrapce: kalendar koji čini grešku od jednog dana u četiri hiljade godine je našoj civilizaciji nepotreban.
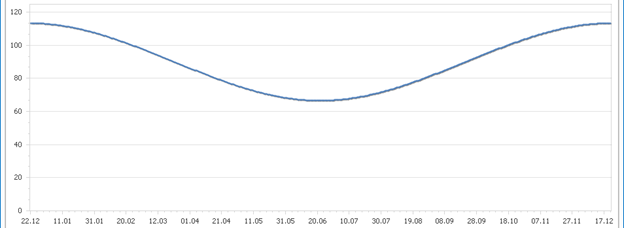
Trajanje dana. Astronomi na Zemlji se ne stide korišćenja naziva koji impliciraju kretanje Sunca oko Zemlje, čime blago čuvaju sećanje na epska vremena Ptolomejeve, geocentrične astronomije. Recimo, vreme potrebno Zemlji da napravi jednu punu rotaciju oko svoje ose astronomi nazivaju Sunčev dan. Administrativno, dan na Zemlji traje 24 časa, ili 86400 sekundi. No, ova vrednost se u astronomiji obično zove srednji Sunčev dan. Trajanje stvarnog Sunčevog dana razikuje se od administrativne vrednosti zbog delovanja nekoliko parametara, od kojih se u standardnim proračunima koriste dva: uticaj iskošenosti Zemljine ose sopstvene rotacije, i ranije pomenuti uticaj promene brzine kretanja Zemlje (a samim tim i trajanja obdanice) tokom godine. Uključivanjem ovih parametara, dobijamo vreme trajanja Sunčevog dana u toku godine:
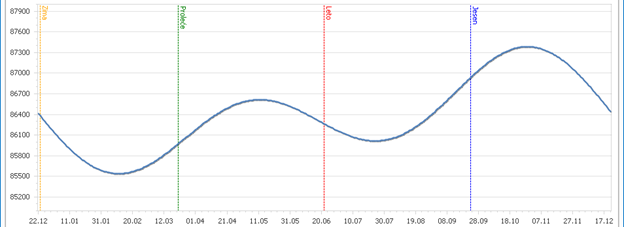
Vidimo da se trajanje dana u toku godine menja tako da se tek četiri puta godišnje administrativno trajanje dana poklapa sa stvarnim Sunčevim danom. Takođe vidimo da tokom godine stvarno trajanje dana može da bude i do 14 minuta kraće, odnosno i do 16 minuta duže od administrativnog.
Položaj tačke na Zemlji. Zbog rotacije Zemlje oko sopstvene, zakošene ose sve što opažamo na nebu moramo vezati za određeno mesto na Zemlji sa koga posmatramo. Ajnštajn u svojoj popularnoj knjizi o relativnosti piše:
Svaki opis mesta događaja ili položaja objekta u prostoru je zasnovan na određivanju tačke na krutom telu (uporednom telu) sa kojom se podudara taj događaj. Ovo se ne odnosi samo na naučni opis, već i na svakodnevni život. Ako analiziram mesto određeno kao u Berlinu, na Potsdamskom Trgu, to znači sledeće. Zemlja je kruto telo na koje se odnosi određivanje mesta; Potsdamski Trg, u Berlinu je jasno definisana tačka, kojoj se dodeljeno ime, i sa kojom se događaj podudara u prostoru.
Mi određujemo mesta na Zemlji koristeći dva podatka: geografsku širinu i geografsku dužinu. Pogledajmo pre svega sliku:
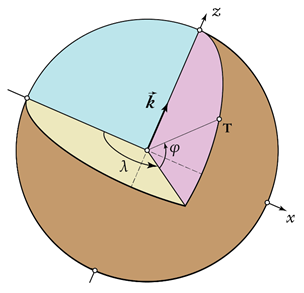
Geografska širina (φ) je ugao od ekvatora do tačke T čiju koordinatu tražimo. Ovaj ugao je pozitivan kada se ide ka severu i negativan kada se ide ka jugu, i kreće se od -90° do +90°. Takođe je popularno i označavanje uglova po hemisferi: Rim ima geografsku širinu 41°54’N, a Pretorija 25°44’S. Geografska širina igra ključnu ulogu u našim razmišljanjima o klimi: sva mesta jednake geografske širine će u toku istog dana u godini biti jednako osunčana.
Geografska dužina (λ) je ugao od Griničkog meridijana do tačke T čiju koordinatu tražimo. Ovaj ugao je uvek pozitivan i kreće se od 0 to 360°, iako se češće koristi označavanje geografskih dužina po strani sveta u odnosu na Grinič. London, logično, ima geografsku dužinu 0°, Rim 12°29’E, a Njujork negde oko 75°W. Geografska dužina je ključni podatak za određivanje mesnog (lokalnog) vremena, o čemu ćemo govoriti kasnije.
Na Zemlji postoje dve specifične oblasti za koje ranije prikazani grafik trajanja Sunčevog dana ne važi. To su geografske širine veće od 66,6° severno i 66,6° južno. Razlog ovome je upravo iskošenost ose Zemljine sopstvene rotacije, što je prikazano na sledećoj slici, koja prikazuje sasvim običan letnji dan severne hemisfere na planeti Zemlji:
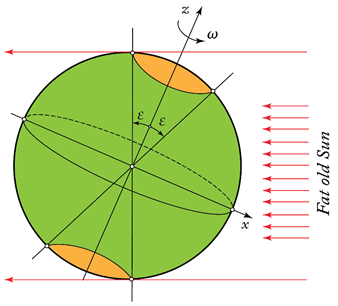
Ugao ε je iskošenost Zemljine ose sopstvene rotacije, odnosno 23,4°. Vidimo da u oblasti geografski širina većih od 90°-ε severno, što odgovara vrednosti od 66,6° i dalje severno, noći ne može biti. Takođe, u oblasti geografski širina većih od 90°-ε južno, što odgovara vrednosti od 66,6° i dalje južno, od obdanice ne može biti ni traga. Ovo je dobar trenutak da malo odmorimo i pogledamo čemu polugodišnja obdanica može da posluži:
Koji je danas dan? Zemlja završi jednu punu rotaciju oko Sunca za godinu dana, odnosno pošto završi 365,2422 obrta oko sopstvene ose rotacije. Ugao nagnutosti Zemljine ose sopstvene rotacije u odnosu na ekliptiku obeležavamo sa γ, i on se može odrediti posmatranjem jednog tekućeg stanja položaja Zemlje u orbiti oko Sunca:
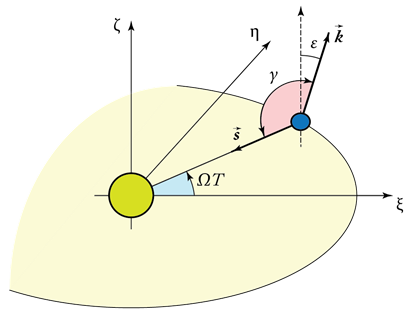
Vidimo da Zemljina sopstvena osa rotacije menja položaj u odnosu na ekliptiku, i to od maksimalnih 90+ ε stepeni u vreme kada je na severnoj polulopti zima, preko tačno 90° u vreme naše prolećne ravnodnevnice, do minimalnih 90- ε stepeni u vreme kada je na severnoj polulopti leto.
Tačan izraz za ugao γ ovde nije bitan, i nećemo ga navoditi. Važno je reći da naš kalendar za prvi dan u godini uzima otprilike onaj dan kada je ugao γ maksimalan, 113,4°. U našoj epohi, taj dan je otprilike 22. decembar. Kalendarski prvi dan u godini (1. januar), dakle, predstavlja istorijski kompromis između maksimalnog otklona Zemljine ose rotacije od ekliptike i perihela, tačke u kojoj se Zemlja nalazi najbliže Suncu (ponovimo, 4. januar). No, u proračunima vezanim za kretanje Zemlje oko Sunca nesumnjivo je prirodno da se za prvi dan u godini uzme upravo 23. decembar.
Koliko je sada sati? Kada stojimo na Zemlji, primećujemo da se Sunce kreće. U jednom trenutku, ono zauzima najvišu tačku na nebu, i tada se obavezno nalazi tačno na jugu. Taj trenutak u toku dana nazivamo mesno (lokalno) podne. To nije okruglo 12 sati na časovniku, jer naši časovnici pokazuju administrativno (zonsko) vreme, koje predstavlja pristojan kompromis, neophodan za vođenje naših dnevnih i teritorijalnih poslova. Tačno mesno (lokalno) vreme dobija se tako što od administrativnog vremena oduzmemo zonski dodatak, pa na tako dobijeno vreme dodamo (u satima) količnik geografske dužine mesta i broja 15. Recimo: administrativno vreme u Beogradu je sada 13:06, a zonski dodatak je +1 sat. Zato je trenutno beogradsko mesno vreme 13:06-01:00+20,48°/15=13:28. Iz ovoga sledi da je mesno vreme u Beogradu 22 minuta veće od administrativnog, što znači da je u Beogradu Sunce tačno na jugu i na najvišoj tački na nebu okruglo u 11:38 po administrativnom vremenu.
Ugao pod kojim u toku dana vidimo Sunce na nebu obeležavamo oznakom α, merimo ga u odnosu na vertikalno poboden štap, a određujemo ga posmatranjem tekućeg stanja tokom dana.
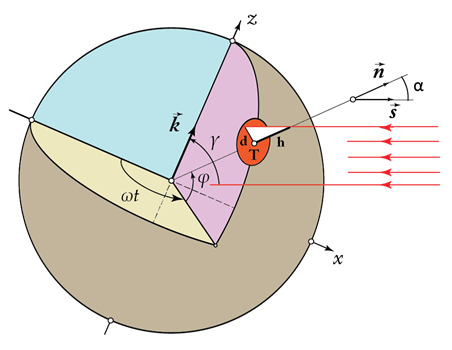
Vidimo da se ugao α kreće od maksimalnih 90° pri izlasku, preko neke minimalne vrednosti u lokalno podne, do ponovno maksimalnih 90° pri zalasku. Sa slike se vidi i da ugao α određuje dužinu senke – ako je u tački T (određenoj geografskom širinom φ i mesnim vremenom t koje je direktno vezano za geografsku dužinu) poboden vertikalni štap dužine h, onda će njegova senka imati dužinu d koja direktno zavisi od tangensa ugla α.
Sledeća slika prikazuje kako se, u Beogradu, kosinus ovog ugla (zašto koristimo kosinus? Sunčev položaj na nebu tokom dana raste od izlaska do podneva, a opada od podneva do zalaska. Na isti način se ponaša kosinus ugla α za razliku od samog ugla, koji tokom dana pre podne opada, a popodne raste) menja tokom dana, i to za četiri različita dana u godini, početak zime, proleća (jeseni) i leta:
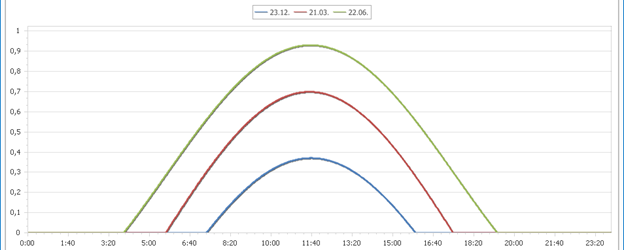
Sa ove slike vidimo da u Beogradu ugao α nikada ne dostiže vrednost 0°, što znači da se u Beogradu ne može desiti da u toku dana nema senke.
Takođe, izraz za ugao α omogućava da se odrede formule za vreme izlaska i zalaska Sunca, kao i posledične obdanice na datom mestu. Takvi izrazi se mogu crtati; evo takvog crteža za slučaj Beograda:
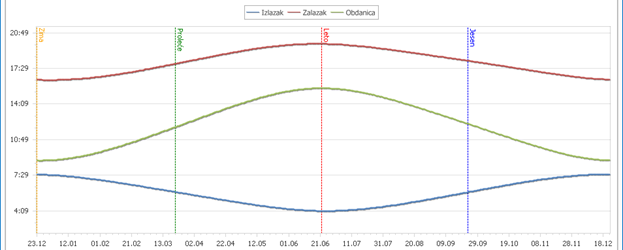
Primetimo da grafik ne uzima u obzir prolećnu administrativnu krađu jednog sata.
Nota bene: Ovaj grafik je dobijen korišćenjem jednostavnog modela sistema Sunce-Zemlje po kome atmosfere nema, Zemlja se u orbiti pomera diskretno (ugao γ se menja jednom dnevno), a dužina dana je korigovana po prethodnim razmatranjima. Kasnije ćemo videti u kojoj meri je ovakav model korektan.
Majka svih nebeskih jednačina. Do sada nismo napisali ni jednu jednačinu. No, sada je pravi trenutak da sa tom praksom prekinemo. Pošto smo opisali tri fundamentalna ugla, α koji se menja svakog trenutka u danu, γ koji se menja svakog dana u godini i geografsku širinu φ koja određuje naše mesto na Zemlji, vreme je da kažemo da u lokalno podne na svakoj tački na Zemlji na kojoj svakog dana u godini Sunce izlazi i zalazi važi sledeća jednačina:
α = γ + φ – 90°
Ova jednačina, koja, budimo otvoreni, važi za bilo koju tačku na bilo kojoj planeti obasjanoj lokalnom zvezdom pod uslovom da u toj tački postoji izlazak i zalazak te lokalne zvezde, može nam pomoći da, samo merenjem senke na razne načine i raznih dana u godini, odredimo karakteristične i dnevne i godišnje parametre. Recimo, dan ravnodnevnice, koji je po definiciji γ=90°, možemo odrediti tako što ćemo merenjem senke u lokalno podne primetiti da je α= φ. Lokalno podne uvek možemo odrediti merenjem senke tako što primetimo trenutak u kome je senka najkraća. Trajanje dana možemo odrediti kao razliku dva trenutka u kojima je senka bila najkraća. Srednja brzina kretanja planete oko lokalne zvezde može se odrediti upoređivanjem dužine dve podnevne senke u danima bliskim ravnodnevnici.
Eratostenov eksperiment, jedan od efektnijih događaja u nauci, kojim se pomoću dužine senke određuje poluprečnik Zemlje, rođen je čitanjem teksta što ga je Eratosten pronašao u Aleksandrijskoj biblioteci, a koji je govorio o mestu po imenu Sijena u kome na početku leta u podne nema senke. Sećamo se: na početku leta γ=66,6°. Ako senke nema, onda je α=0°. Stoga naša nebeska jednačina kaže da geografska širina Sijene mora biti φ=23,4°. Danas se Sijena zove Asuan, a Google Earth javlja da je geografska širina Asuana 24.1°, dakle – taman koliko treba.
Nota bene: Primetimo da tekst nije lagao. A i kako bi mogao? Pisanje je nekada bila retka i skupa privilegija. Zapisivale su se samo one stvari koje je tadašnja kultura smatrala zaista vrednim. Naša potreba da proveravamo zapisano jeste naučna, ali u isto vreme i poučna. Danas se, na razne načine, zapisuju svakakve gluposti, dok kulture nema ni u tragovima. Izvucimo odavde sumorni zaključak: kultura nestaje čim nestane privilegovanost pisanja.
Merenje dužine senke. Videli smo da nam je za određivanje raznih astronomski korisnih stvari potrebno merenje dužine senke vertikalnog štapa pobodenog u horizontalnu podlogu. Kako da to praktično ostvarimo? Horizontalnost podloge možemo proveravati širokom posudom sa vodom, a umesto štapa pobodenog u podlogu možemo konstriusati Eratostenov tripod:

Visak je vertikalan po definiciji pa je jasno da su ovde fotografi u prednosti, jer oni stalno sa sobom vukljaju nekakve tronošce.
Nema razloga da ovakva merenja ne smatramo pouzdanim. Stoga rezultati merenja senke omogućavaju da proverimo naš jednostavni model sistema Sunce-Zemlja. Evo eksperimentalnih podataka za izmereni kosinus ugla α u Beogradu 25. decembra ucrtanih zajedno sa predviđanjima modela:
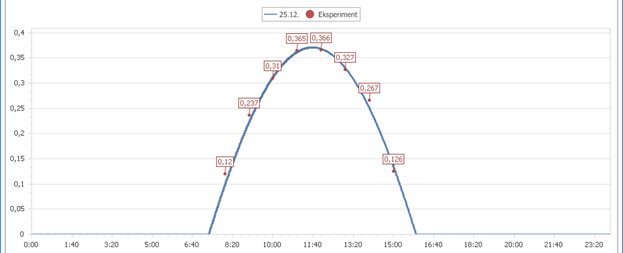
Ovo je klasičan slučaj odličnog slaganja eksperimenta i modela. Sve bolje od prikazanog bi čak bilo i sumnjivo.
Zaključak je sledeći: da bismo korektno modelirali osunčanost Zemlje u toku godine, moramo jedino da vodimo računa o korekciji dužine dana. Ostali parametri (pomeranje Zemlje u orbiti preciznije od dnevnog ili prelamanje Sunčevih zraka pri prolasku kroz Zemljinu atmosferu) su finese koji ne doprinose značajno tačnosti podataka koje model pruža.
Sunčani časovnik. Merenje vremena prvobitno je bilo povezano sa dužinom senke. Iako se za te poslove može iskoristiti štap poboden u podlogu na bilo koji način, najefektniji način za konstruisanje sunčanog časovnika je štap usmeren ka severu koji sa podlogom zaklapa ugao jednak geografskoj širini mesta konstrukcije. Takav štap gleda direktno u zvezdu Severnjaču, što se može lako pokazati. Dužina senke takvog štapa omogućava lako određivanje dnevnog ugla γ, koji je, videli smo, direktno povezan sa trenutnom lokacijom Zemlje u godišnjoj orbiti oko Sunca. Evo slike sa potrebnim elementima za taj proračun koji ovde ipak nećemo izvoditi:
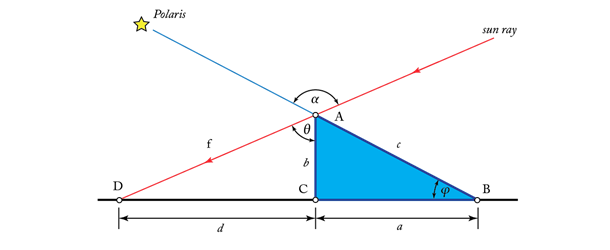
Koincidencijom slučaja, geografska širina Beograda je približno 45°. Stoga se beogradski sunčani časovnik može kupiti u bilo kojoj knjižari, a mi smo svoj našli prekriven prašinom u jednoj fioci:

Kuda na letovanje? Savremene turističke organizacije imaju razrađene sisteme privlačenja klijenata. Udarna mesta u turističkoj reklamokratiji imaju fotografije neba bez oblačka. No, pored toga što lepo izgledaju, šta zapravo takve fotografije prodaju? Ideju o sunčanom. Pogledajmo, stoga, grafik koji pokazuje koliko energije Sunce predaje geografskim širinama tokom određenih dana u godini. Plavo je početak zime, 22. decembar. Crveno je početak proleća, 21. mart. Zeleno je početak leta, 22. jun.
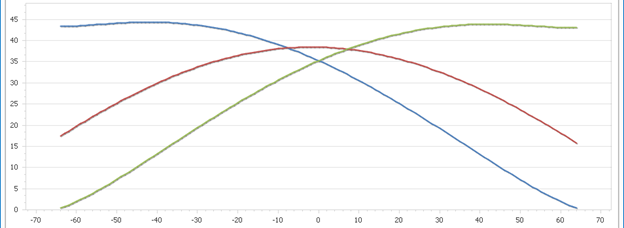
Vidimo da zimski i letnji grafici imaju neočekivani, široki energetski maksimum na geografskim širinama oko 40° (naravno, leti severnim, a zimi južnim) – tačno tamo gde je Evropa, kolevka naših najblistavijih uspona i najmračnijih padova, možda logički prateći Sunčevu energetsku ponudu (vidimo i da se energija na ekvatoru slabo menja: otprilike, tu je gde je).
Pogledajmo i grafik raspodele energije koju određene geografske širine primaju tokom godine:
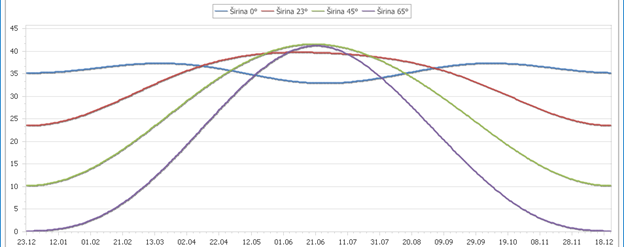
Vidimo punu potvrdu prethodnog grafika: od kraja aprila do kraja avgusta naše geografske širine primaju više energije od monotonog ekvatora, dok je krajnji sever u junu i julu zapravo sasvim pristojno mesto za život – ko preživi šašavi decembar i januar.
I toliko za sada. ![]()

Komentari su onemogućeni.